why is pow(2, 0) 1?

clankill3r

Maybe it's getting late but why is the power of 2 for the value 0 -> 1?

for (int i = 0; i <= 16; i++) {
  println(i, pow(2, i));
}

(Code formatting keeps eating the code...)

clankill3r

Hmm, this forum behaves so strange sometimes with posting code...

bilmor

That code does 2^0 and anything ^0 is 1.

asimes

Nice short math explanation video: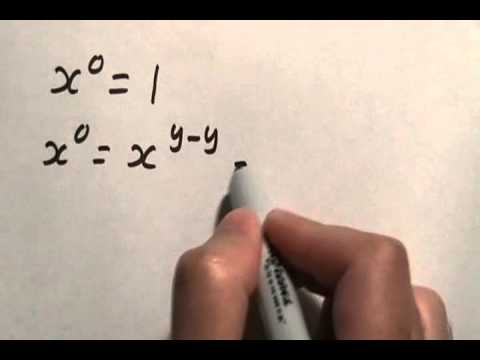

KevinWorkman

Anything to the power of zero is one. That's just a basic (and forgettable) mathematical rule.

x^-3 = 1/(x*x*x)
x^-2 = 1/(x*x)
x ^ -1 = 1/x
x^0 = 1
x^1 = x
x^2 = x*x
x^3 = x*x*x

Get out a calculator and check the value. If you don't have a calculator, try google or Wolfram Alpha.

https://www.google.com/search?q=2^0

http://www.wolframalpha.com/input/?i=2^0

http://www.wolframalpha.com/input/?i=x^0

GoToLoop

x^³ is actually 1 * x*x*x. 1 is the origin, where it all starts.
Likewise x^-³ is 1 / x/x/x.
And x^0 is obviously 1. And it can't be anything else!
For if the origin was 0, the result would be 0 always: 0 * x*x*x.
And any other origin value would alter the result: 2 * x*x*x isn't 1 * x*x*x!

TfGuy44

Please stop saying anything to the 0th power is 0.

0^0 is not 1, it is indeterminate. Thanks.

GoToLoop

0^0 is not 1, it is indeterminate.

That is a special case and nobody was mentioning that 1 in particular:
https://en.Wikipedia.org/wiki/Exponentiation#History_of_differing_points_of_view

"The consensus is to use the definition 0^0=1, although there are textbooks that refrain from defining 0^0."

For when the base in non-zero and exponent is zero, all the explanations were correct:
https://en.Wikipedia.org/wiki/Exponentiation#Zero_exponent
https://en.Wikipedia.org/wiki/Empty_product

KevinWorkman

Please stop saying anything to the 0th power is 0. 0^0 is not 1, it is indeterminate. Thanks.

His original case was only talking about 2^0. We could get into an entire lesson on exponents, but he was only asking why 2^0 is 1.

Interestingly enough, both google and my calculator say 0^0 is 1. Only Wolfram Alpha says 0^0 is indeterminate.

And Processing itself returns 1.0 for pow(0, 0), so from Processing's perspective, 0^0 is indeed 1! :p

quark

Since 0^0 is mathematically indeterminate (Wolfram is right) then Java, Processing and your calculator are technically wrong but it is common to assign 'real values' for mathematically indeterminate values but that doesn't make the value 'right' :)

BTW my calculator reported an error for 0^0 B-)

This video looks at problems associated with the number zero.

KevinWorkman

The original question was simply about why Processing reports 2^0 as 1, and the answer is that Processing reports anything^0 as 1. We've answered the question, and now we're going down a math tangent (get it?).

Processing (er, Java) could have returned NaN for 0^0, but they return 1. I just checked, and so does JavaScript.

But none of this matters to the original question. Processing returns 1 for 2^0 because 2^0 is 1.

quark

The original question was answered in the first comment by bilmor, everything after that is just candyfloss but interesting. :)

_vk

from java's pow():

http://docs.oracle.com/javase/7/docs/api/java/lang/Math.html#pow(double,%20double)

Returns the value of the first argument raised to the power of the second argument. Special cases:
If the second argument is positive or negative zero, then the result is 1.0.
If the second argument is 1.0, then the result is the same as the first argument.
If the second argument is NaN, then the result is NaN.
If the first argument is NaN and the second argument is nonzero, then the result is NaN.
If
the absolute value of the first argument is greater than 1 and the second argument is positive infinity, or
the absolute value of the first argument is less than 1 and the second argument is negative infinity,
then the result is positive infinity.
If
the absolute value of the first argument is greater than 1 and the second argument is negative infinity, or
the absolute value of the first argument is less than 1 and the second argument is positive infinity,
then the result is positive zero.
If the absolute value of the first argument equals 1 and the second argument is infinite, then the result is NaN.
If
the first argument is positive zero and the second argument is greater than zero, or
the first argument is positive infinity and the second argument is less than zero,
then the result is positive zero.
If
the first argument is positive zero and the second argument is less than zero, or
the first argument is positive infinity and the second argument is greater than zero,
then the result is positive infinity.
If
the first argument is negative zero and the second argument is greater than zero but not a finite odd integer, or
the first argument is negative infinity and the second argument is less than zero but not a finite odd integer,
then the result is positive zero.
If
the first argument is negative zero and the second argument is a positive finite odd integer, or
the first argument is negative infinity and the second argument is a negative finite odd integer,
then the result is negative zero.
If
the first argument is negative zero and the second argument is less than zero but not a finite odd integer, or
the first argument is negative infinity and the second argument is greater than zero but not a finite odd integer,
then the result is positive infinity.
If
the first argument is negative zero and the second argument is a negative finite odd integer, or
the first argument is negative infinity and the second argument is a positive finite odd integer,
then the result is negative infinity.
If the first argument is finite and less than zero
if the second argument is a finite even integer, the result is equal to the result of raising the absolute value of the first argument to the power of the second argument
if the second argument is a finite odd integer, the result is equal to the negative of the result of raising the absolute value of the first argument to the power of the second argument
if the second argument is finite and not an integer, then the result is NaN.
If both arguments are integers, then the result is exactly equal to the mathematical result of raising the first argument to the power of the second argument if that result can in fact be represented exactly as a double value.
(In the foregoing descriptions, a floating-point value is considered to be an integer if and only if it is finite and a fixed point of the method ceil or, equivalently, a fixed point of the method floor. A value is a fixed point of a one-argument method if and only if the result of applying the method to the value is equal to the value.)

The computed result must be within 1 ulp of the exact result. Results must be semi-monotonic.