Underdamped Oscillatory Response (Swing doors visual simulation)

processor65

Hi: I wrote this experimental code to perform a visual simulation of an underdamped oscillatory response for swing doors. The purpose is just to obtain an acceptable visual simulation of that physical system with no fancy additions or great art. It's based on my interpretation of the physics and math from this Wikipedia article:http://en.wikipedia.org/wiki/Damping Please let me know if you have any suggestions or find any problems. Here is the video of how it looks: Here is a screen picture:

and here is the code:

Thanks

//Swing doors underdamped oscillatory response (visual simulation test code).
//Built with Processing 2.03 by Adrian Fernandez. Miami, FL. USA. (07-30-2014).
//Based on: http://en.wikipedia.org/wiki/Critically_damped#Critical_damping_.28.CE.B6_.3D_1.29
final float minDampingRatio=0.01;//this code does not work with dampingRatio=0;
final float maxDampingRatio=0.99;
float dampingRatio;//(0<=dampingRatio<1); for under-damping oscillatory response.
final float minFreq=0.25;//for acceptable visual effect on the screen.
final float maxFreq=2;//for acceptable visual effect on the screen.
float freq;// (Hz)  (freq interval (0.5<freq<2.0); for acceptable visual effect.
float A;//equation coeficient
float w0;//angular freq.
float wd;//damped freq (ringing freq);
float B;//equation coeficient
float time=0;//oscillation time in seconds
float initialAngle;//To perform drawings 
float angle;
float doorThickness;
float doorWidth;
float doorHingePositionX;
float doorHingePositionY;
boolean oscillate=false;
int startTime=0;

void setup()
{  
  size(1350, 690);
  frameRate(60);
  dampingRatio=0.1;// 0<=dampingRatio<1; for under-damping oscillatory response.
  //this code does not work with dampingRatio=0;
  final float minA=height/8;
  final float maxA=height/3.2;
  A=200;//initial position in pixels from hinges center.
  float firstDerivativeOfA=0;// Since A is a constant, its first derivative=0
  A=constrain(A, minA, maxA);// to constrain doors size within visual area.  
  dampingRatio=constrain(dampingRatio, minDampingRatio, maxDampingRatio);//For under-damping oscillatory response.
  freq=0.7;// Hz  (freq interval (0.5<freq<1.5) for acceptable visual effect on the screen. 
  freq=constrain(freq, minFreq, maxFreq);// Hz  (freq interval (0.5<freq<1.5)for acceptable visual effect.   
  w0=TWO_PI*freq; //angular freq.
  wd=w0*sqrt(1-sq(dampingRatio));// damped freq (ringing freq);
  B=1/(wd*(dampingRatio*w0*A+firstDerivativeOfA));// coeficient
  doorWidth=A;
  doorThickness=doorWidth/20;
  initialAngle=-HALF_PI;//To perform drawings
}

void draw()
{
  background(0);
  textAlign(CENTER);
  fill(255);  
  textSize(18); 
  text("Swing Doors Underdamped Oscillatory Response. Visual Simulation (top view).", width/2, 50);
  textSize(14);
  text("Damping Ratio= "+dampingRatio+", Freq= "+freq+" Hz", width/2, 80);
  textSize(16);
  text("Click left mouse to swing doors, right to take screen picture.", width/2, height-70);   
  int angleSign=1;    
  drawDoor(angleSign);
  angleSign=-1;// to reverse drawing and rotation
  drawDoor(angleSign);
}

void drawDoor(int angleSign)
{  
  doorHingePositionX=width/2;
  float doorsGap=doorThickness/4;
  doorHingePositionY=height/2-angleSign*(doorWidth+doorsGap); 
  float value=exp(-dampingRatio*w0*time);  
  pushMatrix();
  translate(doorHingePositionX, doorHingePositionY);
  rotate(-initialAngle);
  fill(0, 0, 250);
  noStroke();
  rectMode(CENTER);
  float twiceDoorThickness=2*doorThickness;
  rect(-angleSign*twiceDoorThickness, 0, twiceDoorThickness, twiceDoorThickness);
  rect(-angleSign*3*doorThickness, 0, doorThickness, doorWidth/3);
  if (angleSign==1)
  {
    rotate(initialAngle);// to place text horizontally
    fill(255);
    textAlign(LEFT);
    textSize(18);
    text("time= "+time, 3*doorWidth/2, 0); 
    text(" sec",2*doorWidth+twiceDoorThickness , 0);  
    rotate(-initialAngle);// to restore rotation
  }
  if (value>=0.005&&oscillate)//Stops oscillation when exponential value is 5/1000 from start point.
  {
    float positionY=value*A*cos(wd*time)+B*sin(wd*time);
    time=(millis()-startTime)/1000.0;//seconds
    angle=angleSign*acos(positionY/doorWidth);
  }
  else
  { 
    angle=-angleSign*initialAngle;
    oscillate=false;
  }
  rotate(angle+initialAngle);
  rectMode(CORNER);
  fill(0, 0, 250); 
  rect(doorThickness, doorThickness/2, doorWidth-doorThickness, -doorThickness);
  stroke(255);
  strokeWeight(doorThickness); 
  ellipse(0, 0, twiceDoorThickness, twiceDoorThickness);
  popMatrix();
}

void mouseClicked()
{
  if (mouseButton==LEFT)
  {
    oscillate=true;
    startTime=millis();// resets timer
    time=0;// resets time
  }
  if (mouseButton==RIGHT)
  {
    save("Underdamped Oscillatory_Response(Dratio= "+dampingRatio+",Freq= "+freq+"Hz, time= "+time+").png");// saves a screen picture in the sketch folder.
  }
}

processor65

Hi:

I did a few modifications and added a simple graph to observe the response.

This is an experimental code to simulate a swing door under damped oscillatory response and a simple graph. Most of the variables are global and interrelated for easy substitution. Although, I have not tested all possible values for the variables they and the graph are custom made for this particular example. Please let me know if you find any problems. Based on my interpretation from this Wikipedia article: http://en.wikipedia.org/wiki/Damping Built with Processing 2.03.

here is the video: Thanks.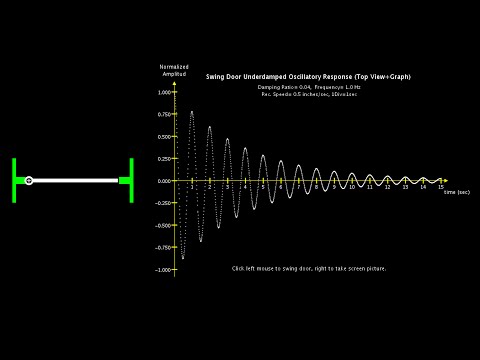

processor65

Hi:

Here is an update for this code. Added peaks calculation in real time, drawing the exponentials and continuous graph with lines instead of points. Due to the discrete nature of the computational process, which does not allow for infinitesimal sampling, there are intrinsic inaccuracies in the peaks detection process. They are dependent on the sampling freq, which is affected by the frameRate(), the slope of the graph and the graph speed. I haven't tested all the possibilities of the variables. Most of them are global and interrelated to facilitate substitution. Please let me know if you have suggestions or find problems.

The goal was to obtain an acceptable visual effect.

here is the code:

//Swing door underdamped oscillatory response + Graph (visual simulation test code update 1).
//Built with Processing 2.03 by Adrian Fernandez. Miami, FL. USA. (Aug.-10-2014).
//Based on: http://en.wikipedia.org/wiki/Damping
final float minDampingRatio=0.01;//this code does not work with dampingRatio=0;
final float maxDampingRatio=0.2;//for acceptable visual effect on graph.
float dampingRatio;//(0<=dampingRatio<1); for under-damping oscillatory response.
final float minFreq=0.25;//for acceptable visual effect on the screen.
final float maxFreq=2;//for acceptable visual effect on the screen.
float freq;// (Hz)  (freq interval 0.5<freq<2.0); for acceptable visual effect.
float initialA;//initial equation coeficient
float A;//equation coeficient
float absA;//equation coeficient absolute value
float w0;//angular freq.
float wd;//damped freq (ringing freq);
float B;//equation coeficient
float time;//oscillation time in seconds
int startTime;//oscillation start time
float positionY; 
float positionX;
float previousPositionX;
float graphHorizZero;
float graphVertZero;
float graphWidth;
float graphHeight;
int graphSpeed;
float peakPositionX;
float peakPositionY;
boolean drawGraphFlag=false;  
float doorHingePositionX;
float doorHingePositionY;
float doorThickness;
float doorWidth;
final float initialAngle=HALF_PI;
float angle=-initialAngle;
float currentSlope;
String oscillatoryResponseType="Swing Door Underdamped Oscillatory Response (Top View+Graph Update 1) ";
String stringToText="Click left mouse to swing door.";
int backgroundColor=0;

void setup()
{  
  size(1350, 690);
  frameRate(100);
  dampingRatio=0.05;// 0<=dampingRatio<1; for under-damping oscillatory response.
  dampingRatio=constrain(dampingRatio, minDampingRatio, maxDampingRatio);//for under-damping oscillatory response.
  //this code does not work with dampingRatio=0;
  final float minA=height/6;
  final float maxA=height/2.75;
  initialA=300;
  initialA=constrain(initialA, minA, maxA);// to constrain doors size withing visual area.  
  A=initialA;//initial position in pixels from hinges center.
  float firstDerivativeOfA=0;// Since A is a constant, its first derivative=0
  //A=-A;//reverses initial position.
  absA=abs(A);
  dampingRatio=constrain(dampingRatio, minDampingRatio, maxDampingRatio);//For under-damping oscillatory response.
  freq=1;// Hz  (freq interval (0.5<freq<1.5) for acceptable visual effect on the screen. 
  freq=constrain(freq, minFreq, maxFreq);// Hz  (freq interval (0.5<freq<1.5)for acceptable visual effect.   
  w0=TWO_PI*freq; //angular freq.
  wd=w0*sqrt(1-sq(dampingRatio));// damped freq (ringing freq);
  B=1/(wd*(dampingRatio*w0*A+firstDerivativeOfA));// coeficient
  doorWidth=absA;
  doorThickness=doorWidth/25;
  graphHeight=absA+2*doorThickness;
  graphSpeed=50;//pixels/sec
  graphVertZero=height/2;
  graphHorizZero=2*doorWidth-doorThickness;
  graphWidth=width-graphHorizZero-100;
  doorHingePositionY=graphVertZero;
  doorHingePositionX=graphHorizZero/6;
  drawAxis();
  textHeader();
}

void draw()
{
  drawDoor();  
  textInstructions();
  if (drawGraphFlag)
  {
    drawGraph();
  }
}

void drawAxis()
{
  background(backgroundColor); 
  stroke(255, 255, 0);
  strokeWeight(1); 
  line(graphHorizZero, graphVertZero+graphHeight, graphHorizZero, graphVertZero-graphHeight);
  fill(255, 255, 0);
  triangle(graphHorizZero-4, graphVertZero-graphHeight, graphHorizZero+4, graphVertZero-graphHeight, graphHorizZero, graphVertZero-graphHeight-8);
  line(graphHorizZero-5, graphVertZero, graphHorizZero+graphWidth, graphVertZero); 
  triangle(graphHorizZero+graphWidth, graphVertZero-4, graphHorizZero+graphWidth, graphVertZero+4, graphHorizZero+graphWidth+8, graphVertZero); 
  strokeWeight(2);
  fill(255);
  textSize(13);
  textAlign(RIGHT, CENTER);
  for (int i=-4;i<5;i++)//Amplitude scale
  { 
    line(graphHorizZero-7, graphVertZero+i*absA/4, graphHorizZero+7, graphVertZero+i*absA/4);  
    text((-i/4.0), graphHorizZero-10, graphVertZero+i*absA/4);
  }
  textAlign(CENTER, TOP);
  for (int i=1;i<graphWidth/graphSpeed;i++)//time scale
  {
    line(graphHorizZero+i*graphSpeed, graphVertZero-7, graphHorizZero+i*graphSpeed, graphVertZero+7);
    text(i, graphHorizZero+i*graphSpeed, graphVertZero+10);
  }
  textSize(15);
  text("Normalized", graphHorizZero, graphVertZero-graphHeight-60);
  text("Amplitud", graphHorizZero, graphVertZero-graphHeight-40);
  textAlign(LEFT, CENTER);
  text("time (sec)", graphHorizZero+graphWidth, graphVertZero+30);
}

void textHeader()
{ 
  rectMode(CENTER);
  float spacing=25; 
  float headerPositionX=graphHorizZero+graphWidth/2+40;
  float headerPositionY=2*spacing;
  float headerWidth=graphWidth-60; 
  float headerHeight=4*spacing;
  fill(backgroundColor);
  noStroke(); 
  rect(headerPositionX, headerPositionY+spacing, headerWidth, headerHeight);
  fill(255);
  textSize(18);
  textAlign(CENTER, CENTER);
  text(oscillatoryResponseType, headerPositionX, headerPositionY);
  textSize(14);
  text("Initial Amplitude= "+(A/initialA)+",  Damping Ratio= "+dampingRatio+",  Frequency= "+freq+" Hz", headerPositionX, headerPositionY+spacing);
  text("Rec. Speed= "+map(graphSpeed, 0, 100, 0, 1)+" inches/sec, 1Div=1sec", headerPositionX, headerPositionY+2*spacing);//screen 100 pixels/inch
}

void drawGraph()
{
  time=(millis()-startTime)/1000.0;// time in sec
  float previousPreviousPositionX=previousPositionX;
  float previousPositionY=positionY;
  previousPositionX=positionX;
  float argument1=-dampingRatio*w0*time;
  float argument2=wd*time; 
  positionY=exp(argument1)*A*cos(argument2)+B*sin(argument2); 
  positionX=graphHorizZero+time*graphSpeed;
  float vertPosition=graphVertZero+positionY;
  findAndDrawPeaks(previousPositionY, previousPreviousPositionX);
  stroke(255);
  strokeWeight(1);
  line(positionX, vertPosition, previousPositionX, graphVertZero+previousPositionY);    
  stringToText="";  
  if (positionX<=(graphHorizZero+graphWidth-10)&&drawGraphFlag)
  {       
    stringToText="Recording response!";
  }
  else
  {
    if (abs(A)>initialA/2)
    {
      reStartGraph();
    }
    else
    {      
      A=initialA;    
      drawAxis();
      reStartGraph();
    }
  }
}

void findAndDrawPeaks(float previousPositionY, float previousPreviousPositionX)
{
  float previousSlope=currentSlope;
  currentSlope=(positionY-previousPositionY)/(positionX-previousPositionX);
  float previousPeakPositionX=peakPositionX;
  float previousPeakPositionY=peakPositionY;
  if (currentSlope*previousSlope<=0)//if first derivative changes sign (to find peak)
  {
    peakPositionX=(previousPreviousPositionX+positionX)/2; //interpolating (aprox) new peak X ocurrence;
    float  peakPositionXTime=(peakPositionX-graphHorizZero)/graphSpeed;//calculating peak time occurence
    float argument3=-dampingRatio*w0*peakPositionXTime;
    float argument4=wd*peakPositionXTime;
    peakPositionY=exp(argument3)*A*cos(argument4)+B*sin(argument4); //calculating new peak Y from interpolated time.
    //noStroke();
    //fill(255, 0, 0);    
    //ellipse(peakPositionX, graphVertZero+peakPositionY, 6, 6 ); 
    //ellipse(peakPositionX, graphVertZero-peakPositionY, 6, 6 );
    stroke(255, 0, 0);
    strokeWeight(2);
    line(previousPeakPositionX, graphVertZero+previousPeakPositionY, peakPositionX, graphVertZero-peakPositionY);
    line(previousPeakPositionX, graphVertZero-previousPeakPositionY, peakPositionX, graphVertZero+peakPositionY);
    stroke(0, 0, 255);
    float beamWidth=A/25;
    line(previousPeakPositionX, graphVertZero+previousPeakPositionY+beamWidth, peakPositionX, graphVertZero-peakPositionY-beamWidth);
    line(previousPeakPositionX, graphVertZero-previousPeakPositionY-beamWidth, peakPositionX, graphVertZero+peakPositionY+beamWidth);
  }
}

void textInstructions()
{
  fill(backgroundColor);
  noStroke();
  rectMode(CENTER);
  float textSize=15;
  float instructionPositionX=graphHorizZero+graphWidth/2+40; 
  float instructionPositionY=height-100;
  rect(instructionPositionX,instructionPositionY , graphWidth-200, 2*textSize);//Erases old mouse instructions 
  textSize(textSize);
  textAlign(CENTER, CENTER);
  fill(255);  
  text(stringToText, instructionPositionX, instructionPositionY);// texts new mouse instructions
}

void drawDoor()
{ 
  float halfDoorThickness=doorThickness/2;
  float twiceDoorThickness=2*doorThickness;
  fill(backgroundColor);
  noStroke();
  rectMode(CENTER); 
  pushMatrix();
  translate(doorHingePositionX, doorHingePositionY);
  rect(doorWidth/2-doorThickness/8, 0, doorWidth+9*doorThickness, 2*(absA+doorThickness));//clears door background 
  rectMode(CORNER); 
  fill(0, 255, 0);
  rect(-doorThickness, doorThickness, -3*doorThickness, -twiceDoorThickness);
  rect(-4*doorThickness+doorThickness/3, -doorWidth/4, -doorThickness, doorWidth/2);
  rect(doorWidth+3*doorThickness+doorThickness/3, doorThickness, -3*doorThickness, -twiceDoorThickness);
  rect(doorWidth+doorThickness/3+4*doorThickness, -doorWidth/4, -doorThickness, doorWidth/2); 
  if (drawGraphFlag)
  {
    angle=-acos(positionY/doorWidth);
  }
  else
  {
    angle=-initialAngle;
  }      
  rotate(angle+initialAngle);
  fill(255);
  rect(doorThickness, halfDoorThickness, doorWidth-doorThickness, -doorThickness);
  strokeWeight(halfDoorThickness);
  stroke(255); 
  noFill();
  ellipse(0, 0, twiceDoorThickness, twiceDoorThickness);
  strokeWeight(doorThickness/5);  
  line(-halfDoorThickness, 0, halfDoorThickness, 0);//screw
  rotate(HALF_PI);
  line(-halfDoorThickness, 0, halfDoorThickness, 0);//screw
  popMatrix();
}

void mouseClicked()
{
  if (drawGraphFlag==false)
  {
    if (mouseButton==LEFT)
    {
      reStartGraph();
    }
  }
}

void reStartGraph()
{ 
  drawGraphFlag=true;
  positionX=graphHorizZero;
  A=-0.9*A;
  currentSlope=A;
  peakPositionX=graphHorizZero;  
  textHeader(); 
  startTime=millis();
}

processor65

I think its better for calculating the peaks to find when the slope changes sign only and not also when it equals zero. The equal zero situation remained there from previous tests I was trying and forgot to remove as it is hard to differentiate the visual results, sorry. Please beware that this method to calculate the peaks, works for this particular mathematical function; but it may not be suited for others, like for example those having constant values for extended periods of time (where the slope is zero) or when the function has poles in the interval being analyzed.

Then the find and draw peaks function with the (=) removed from the if() should be:

void findAndDrawPeaks(float previousPositionY, float previousPreviousPositionX)
{
  float previousSlope=currentSlope;
  currentSlope=(positionY-previousPositionY)/(positionX-previousPositionX);
  float previousPeakPositionX=peakPositionX;
  float previousPeakPositionY=peakPositionY;
  if (currentSlope*previousSlope<0)//if first derivative changes sign (to find peak)
  {
    peakPositionX=(previousPreviousPositionX+positionX)/2; //interpolating (aprox) new peak X ocurrence;
    float  peakPositionXTime=(peakPositionX-graphHorizZero)/graphSpeed;//calculating peak time occurence
    float argument3=-dampingRatio*w0*peakPositionXTime;
    float argument4=wd*peakPositionXTime;
    peakPositionY=exp(argument3)*A*cos(argument4)+B*sin(argument4); //calculating new peak Y from interpolated time.
    //noStroke();
    //fill(255, 0, 0);    
    //ellipse(peakPositionX, graphVertZero+peakPositionY, 6, 6 ); 
    //ellipse(peakPositionX, graphVertZero-peakPositionY, 6, 6 );
    stroke(255, 0, 0);
    strokeWeight(2);
    line(previousPeakPositionX, graphVertZero+previousPeakPositionY, peakPositionX, graphVertZero-peakPositionY);
    line(previousPeakPositionX, graphVertZero-previousPeakPositionY, peakPositionX, graphVertZero+peakPositionY);
    stroke(0, 0, 255);
    float beamWidth=A/25;
    line(previousPeakPositionX, graphVertZero+previousPeakPositionY+beamWidth, peakPositionX, graphVertZero-peakPositionY-beamWidth);
    line(previousPeakPositionX, graphVertZero-previousPeakPositionY-beamWidth, peakPositionX, graphVertZero+peakPositionY+beamWidth);
  }
}

Thanks.

processor65

here is the video of how it works:

And this is a screen picture of the end result: