Howdy, Stranger!
We are about to switch to a new forum software. Until then we have removed the registration on this forum.
Categories
- All Categories 25.7K
- Announcements & Guidelines 13
- Common Questions 30
- Using Processing 22.1K
- Programming Questions 12.2K
- Questions about Code 6.4K
- How To... 4.2K
- Hello Processing 72
- GLSL / Shaders 292
- Library Questions 4K
- Hardware, Integration & Other Languages 2.7K
- Kinect 668
- Arduino 1K
- Raspberry PI 188
- Questions about Modes 2K
- Android Mode 1.3K
- JavaScript Mode 413
- Python Mode 205
- Questions about Tools 100
- Espanol 5
- Developing Processing 548
- Create & Announce Libraries 211
- Create & Announce Modes 19
- Create & Announce Tools 29
- Summer of Code 2018 93
- Rails Girls Summer of Code 2017 3
- Summer of Code 2017 49
- Summer of Code 2016 4
- Summer of Code 2015 40
- Summer of Code 2014 22
- p5.js 1.6K
- p5.js Programming Questions 947
- p5.js Library Questions 315
- p5.js Development Questions 31
- General 1.4K
- Events & Opportunities 288
- General Discussion 365
In this Discussion
- jeremydouglass January 2018
- kfrajer January 2018
- PJMcPrettypants January 2018
Continuous Eased Flip/Rotation
I want to move a shape around in 3D continuously, but I want it to spend most of the time close to perpendicular to the camera.
I'm looking for a motion something like this:
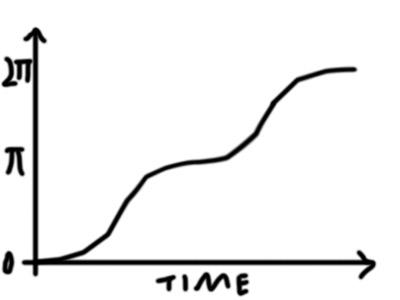
I have the following code, which does what I want it do for now:
int flipTime;
float rotation;
void setup() {
size(400, 400, P3D);
rotation = 0.0;
flipTime = 100;
}
void draw() {
background(128);
translate(200, 200, 20);
if ( (frameCount % flipTime) < (flipTime/2) ) {
rotation = HALF_PI * ( 1+ sin( ( (frameCount % (flipTime/2)) * PI / (flipTime/2) ) -HALF_PI) );
} else {
rotation = PI + (HALF_PI * ( 1+ sin( ( (frameCount % (flipTime/2)) * PI / (flipTime/2) ) -HALF_PI) ));
}
rotateY(rotation);
fill(255);
box(200, 200, 20);
fill(0);
translate(0, 0, -20);
box(200, 200, 20);
}
However, the if/else structure seems like it's going to make things complicated further down the line. I'd like to stack many such rotations and translations on different axes and apply them to the same object, all out of phase with each other, and be able to tweak the variables, maybe using sin(x)^3, sin(x)^5 etc. for more eased motion.
Is there a more elegant way to do this?
Also, is there a page somewhere that gives examples on how to manipulate sine functions for these kinds of purposes? Something like the Trigonometry Primer, but part 2?

Answers
A demo in 2D below.
Step 1: Different rotations on different axis
Step 2: Those rotations out of phase wrt each other
For step 1:
rotateY(rotation);
rotateX(rotation);
rotateZ(rotation);
For step 2:
rotateY(rotation+phaseY);
rotateX(rotation+phaseX);
rotateZ(rotation+phaseZ);
where the phases are defined in setup().
Kf
@PJMcPrettypants -- instead of components, let's try an additive approach -- superimposing waves. Rotate your graph by 45 degrees and look at it. It looks like a flat sine wave, right? https://en.wikipedia.org/wiki/Sine_wave
Now we just need to put it on a slope. Here is a slope:
...so let's have the waves go up and down from that slope as the baseline:
But what if the slope is too steep -- you wanted it to take longer!
Ok, but that curve is way too loud! Let's make the sign wave flatter by dropping the amplitude, just like we would if it wasn't on a curve:
...but wait -- the frequency needs to be higher, and the phase isn't aligning the curves correctly! No problem -- just manipulate f and p in your sine component to change alignment....
To play around with settings on a labeled graph, drop this into the setup() of the grafica DefaultPlot sketch and start tweaking settings:
Note that this particular approach (sin + x=y) may not specifically work out for what you have in mind, but it gives you a general idea of how to add things together to get a motion profile.
Thanks to both of you.
One thing that tripped me up with the linear plus sine function was trying to change the variables but keep the flat parts of the curve locked in on 0, pi, 2pi, etc.
What I didn't realise was that the frequency and slope have to stay in proportion to one another to hit those spots.
So in
y(t) = slope*t + A*sin(f*t+p)frequency has to be 2*slope.
Also phase has to be pi, and if amplitude goes over 0.5 the rotation will change direction rather than just slow down.
So it could be written as
y(t) = slope*t + 0.5*sin(slope*2*t+PI)I've changed my original sketch so that the rotation time is controlled by mouseX:
@PJMcPrettypants -- Thanks for sharing your solution and demo! Very nice timed flipping effect.